C语言字符串的模式匹配之BF与KMP
时间：2022-12-05确定一个子串（模式串）在主串中第一次出现的位置。
BF算法（Brute-Force算法）
BF算法即朴素的简单匹配法，采用的是穷举的思路。从主串的每一个字符开始依次与模式串的字符进行比较。
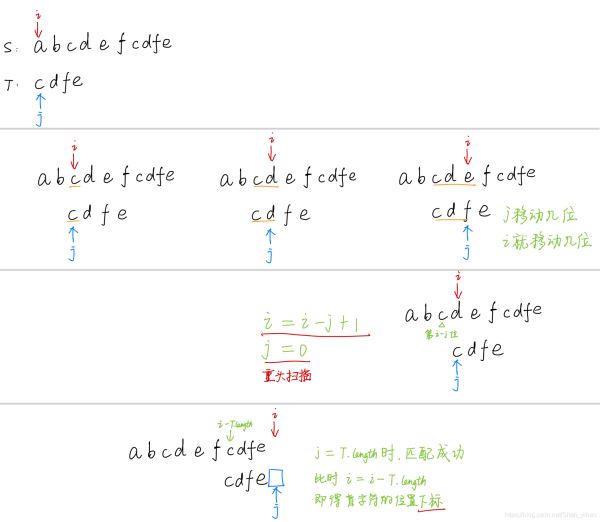
int index_BF(SeqString S, SeqString T, int begin)//从S的第begin位（下标）开始进行匹配判断
{
int i = begin, j = 0;
while (i < S.length && j < T.length)
{
if (S.ch[i] == T.ch[j])
{
i ++;
j ++;//比较下一个字符
}
else
{
i = i - j + 1;
j = 0;//模式串回溯到起点
}
}
if (j == T.length) return i - T.length; //匹配成功，则返回该模式串在主串中第一次出现的位置下标
else return -1;
}
int index_BF(char S[], char T[], int beg)
{
int i = beg, j = 0;
while (i < strlen(S) && j < strlen(T))
{
if (S[i] == T[j])
{
i ++;
j ++;
}
else
{
i = i - j + 1;
j = 0;
}
}
if (i == strlen(S)) return i - strlen(T);
else return -1;
}
int main()
{
char str1[10] = "abcde";
char str2[10] = "cde";
printf("%d", index_BF(str1, str2, 0));
return 0;
}
KMP算法（快速的）
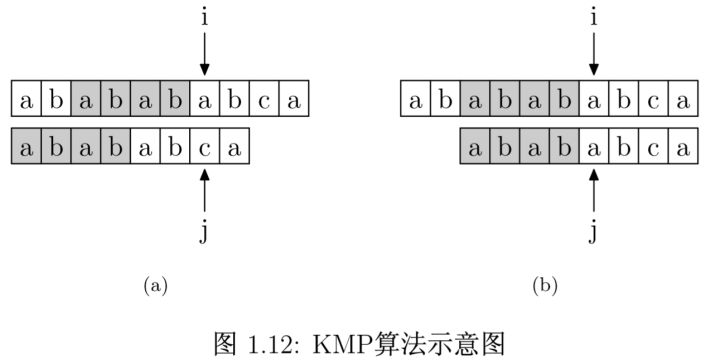
基本思想为：主串的指针 i i i不必回溯，利用已经得到前面“部分匹配”的结果，将模式串向右滑动若干个字符，继续与主串中的当前字符进行比较，减少了一些不必要的比较。
时间复杂度为 O ( n + m )
KMP算法的核心，是一个被称为部分匹配表(Partial Match Table)的数组。
首先要明白什么是字符串的前缀和后缀。
如果字符串A和B，存在A=BS，其中S是任意的非空字符串，那就称B为A的前缀。例如，”Harry”的前缀包括{”H”, ”Ha”,”Har”, ”Harr”}，我们把所有前缀组成的集合，称为字符串的前缀集合。
同样可以定义后缀A=SB，其中S是任意的非空字符串，那就称B为A的后缀，例如，”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”}，然后把所有后缀组成的集合，称为字符串的后缀集合。
要注意的是，字符串本身并不是自己的前缀或后缀。
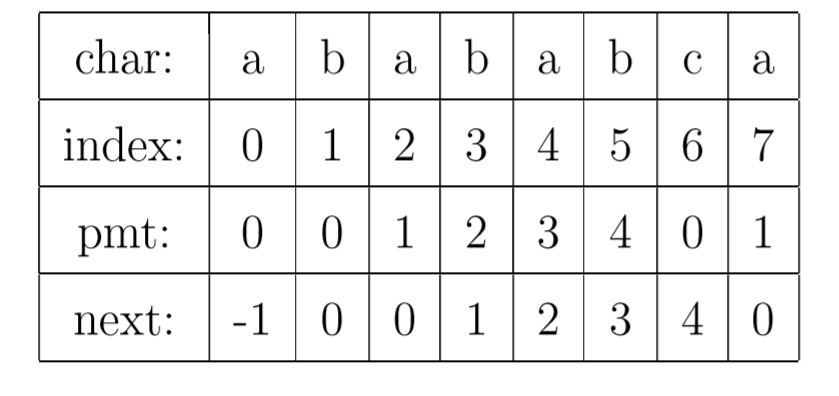
PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
比如，对于字符串”ababa”，它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”}，它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}， 两个集合的交集为{”a”, ”aba”}，其中最长的元素为”aba”，长度为3，即该字符串在PMT表中的值为3。性质为：该字符串前3个字符与后三个字符相同。
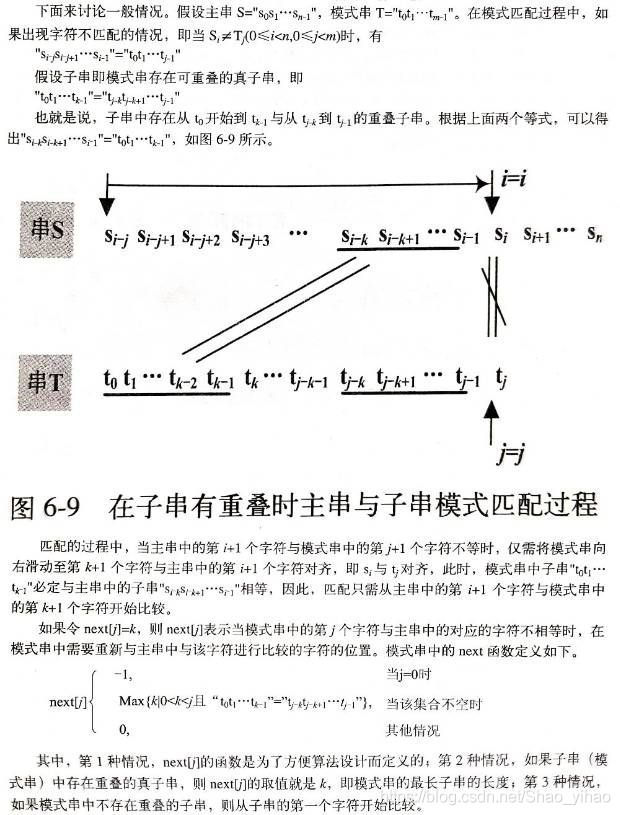
如果模式串有 j个字符，则PMT表中就有 j 个数值。其中第一个数值总为0。
int index_KMP(SeqString S, SeqString T, int begin)//从S的第begin位（下标）开始进行匹配判断
{
int i = begin, j = 0;
while (i < S.length && j < T.length)
{
if (j == -1 || S.ch[i] == T.ch[j])
{
i ++;
j ++;
}
else j = next[j];//即PMT[j-1]
}
if (j == T.length) return i - T.length; //匹配成功，则返回该模式串在主串中第一次出现的位置下标
else return -1;
}
那么该如何求出next数组呢？
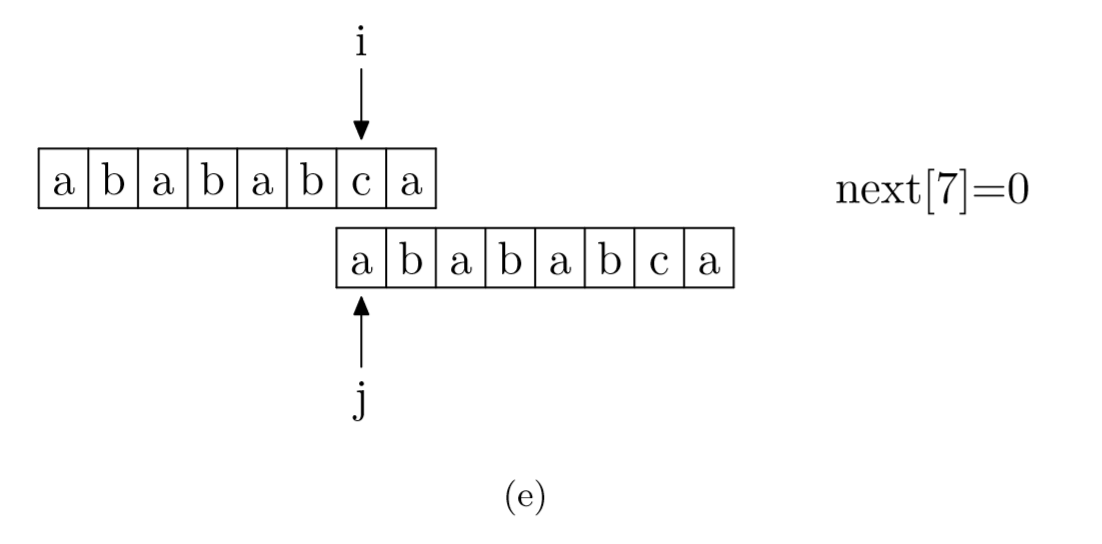
其实，求next数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度。
具体来说，就是从模式字符串的第一位(注意，不包括第0位)开始对自身进行匹配运算。 在任一位置，能匹配的最长长度就是当前i位置的next值。如下图所示。
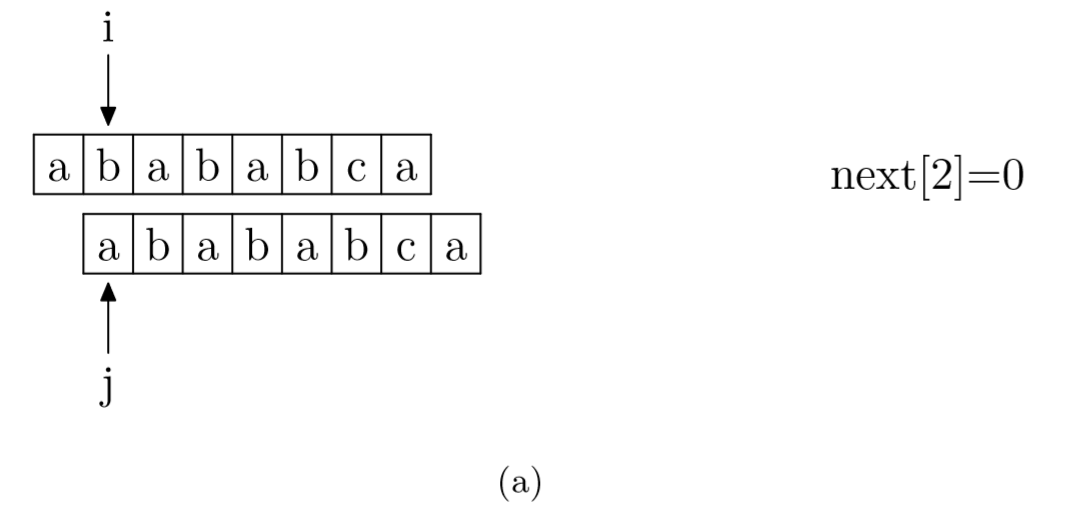
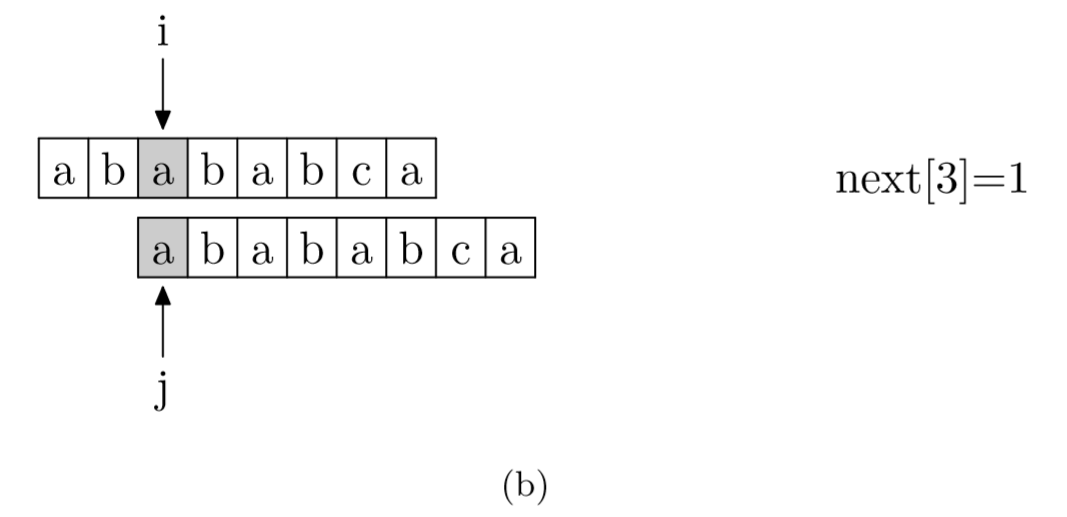
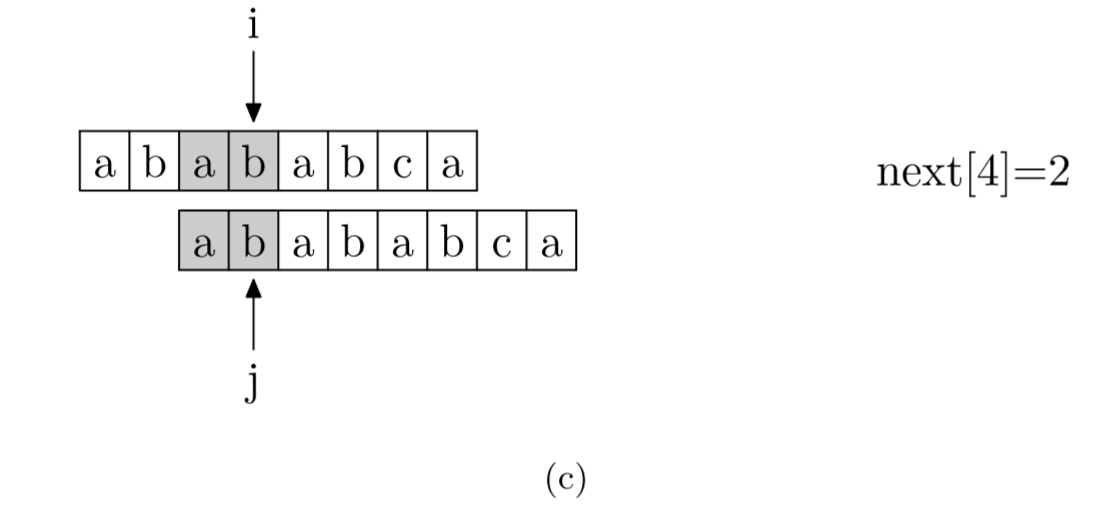
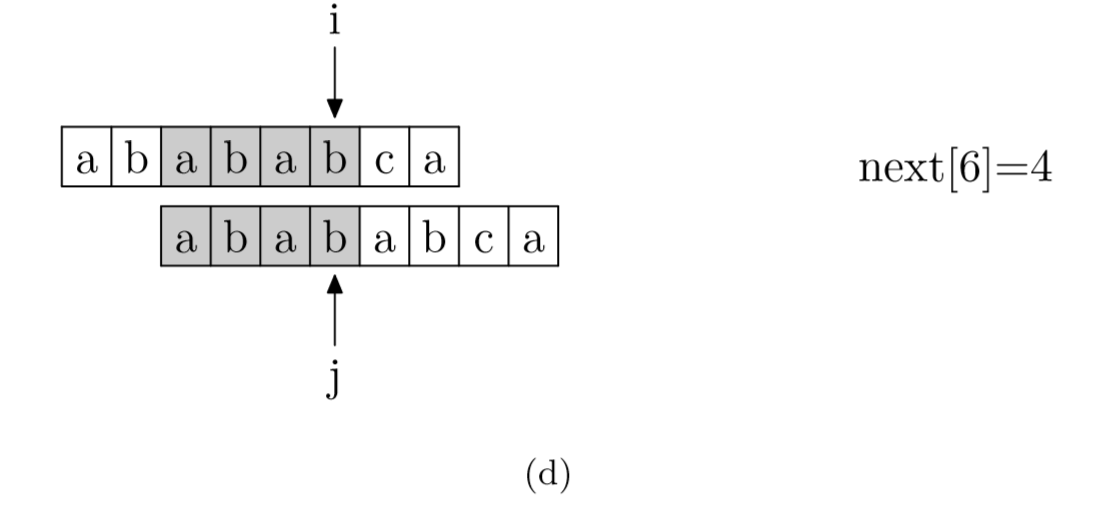
void GetNext(SeqString T, int next[])
{
next[0] = -1;
int j = 0, k = -1;//起始时k落后j一位
while (j < T.length)//j遍历一遍模式串，对于每个字符得到该位置的next数组的值
{
if (k == -1 || T.ch[j] == T.ch[k])
{
j ++;
next[j] = k + 1;//将j视为指向一个子串（后缀）结束后的下一个字符，k指向一个子串（前缀）的最后一个字符，则这两个子串的重叠部分的长度（k下标从0开始）即PMT[j-1]的值
k ++;
/*也可以简便地写为（易记）：
j ++;
k ++;
next[j] = k;
最简单的形式为：
next[++ j] = ++ k;
*/
}
else k = next[k];//k回溯，即将第二个子串（右滑）（减小匹配的前缀长度）
}
}
即：
#include <stdio.h>
#include <string.h>
int next[10];//全局数组
void GetNext(char T[])
{
int j = 0, k = -1;
next[0] = -1;
while (j < strlen(T))
{
if (k == -1 || T[j] == T[k])
{
j ++;
next[j] = k + 1;
k ++;
}
else k = next[k];
}
}
int index_KMP(char S[], char T[], int begin)//从S的第begin位（下标）开始进行匹配判断
{
int i = begin, j = 0;
while (i < strlen(S) && strlen(T))
{
if (j == -1 || S[i] == T[j])
{
i ++;
j ++;
}
else j = next[j];//即PMT[j-1]
}
if (j == strlen(T)) return i - strlen(T); //匹配成功，则返回该模式串在主串中第一次出现的位置下标
else return -1;
}
int main()
{
char str1[10] = "abcde";
char str2[10] = "cde";
GetNext(str2);
printf("%d", index_KMP(str1, str2, 0));
return 0;
}
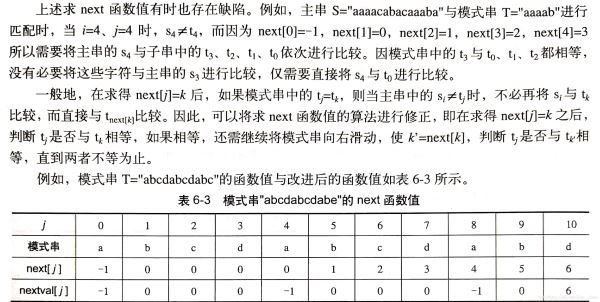
求next数组的方法也可进行优化：
void GetNextVal(SeqString T, int nextval[])
{
nextval[0] = -1;
int j = 0, k = -1;
while (j < T.length)
{
if (k == -1 || T.ch[j] == T.ch[k])
{
j ++;
k ++;
if (T.ch[j] != T.ch[k])
nextval[j] = k;
else
nextval[j] = nextval[k];
}
else k = nextval[k];
}
}
即：
int nextval[10];//全局数组
void GetNextVal(char T[])
{
int j = 0, k = -1;
nextval[0] = -1;
while (j < strlen(T))
{
if (k == -1 || T[j] == T[k])
{
j ++;
k ++;
if (T[j] != T[k]) nextval[j] = k;
else nextval[j] = nextval[k];
}
else k = nextval[k];
}
}
int index_KMP(char S[], char T[], int begin)//从S的第begin位（下标）开始进行匹配判断
{
int i = begin, j = 0;
while (i < strlen(S) && strlen(T))
{
if (j == -1 || S[i] == T[j])
{
i ++;
j ++;
}
else j = nextval[j];
}
if (j == strlen(T)) return i - strlen(T); //匹配成功，则返回该模式串在主串中第一次出现的位置下标
else return -1;
}
int main()
{
char str1[10] = "abcde";
char str2[10] = "bcde";
GetNextVal(str2);
printf("%d", index_KMP(str1, str2, 0));
return 0;
}
KMP—yxc模板
字符串从数组下标1开始存
#include <iostream>
using namespace std;
const int M = 1000010, N = 100010;
char S[M], p[N];
int ne[N]; //全局变量数组，初始化全为0
int main()
{
int m, n;
cin >> m;
for (int i = 1; i <= m; i ++) cin >> S[i];
cin >> n;
for (int i = 1; i <= n; i ++) cin >> p[i];//主串与模式串均由数组下标1开始存储
// 也可以简写为 cin >> m >> S + 1 >> n >> p + 1;
for (int i = 2, j = 0; i <= n; i ++)//求模式串各字符处的next值，即求串p[1~i]的前后缀最大交集的长度
{ //由于字符串由下标1开始存储，next[i]+1也是模式串下次比较的起始下标
while (j && p[i] != p[j + 1]) j = ne[j];//记录的最大交集的长度减小，直到为0，表示p[1~i]前后缀无交集
if (p[i] == p[j + 1]) j ++;//该位匹配成功
ne[i] = j;//j即该位的ne值
}
for (int i = 1, j = 0; i <= m; i ++)//遍历一遍主串
{
while (j && S[i] != p[j + 1]) j = ne[j];//不匹配且并非无路可退，则j后滑。j==0意味着当前i所指的字符与模式串的第一个字符都不一样，只能等该轮循环结束i++，之后再比较
if (S[i] == p[j + 1]) j ++;//该位匹配成功
if (j == n)//主串与模式串匹配成功
{
cout << i - n << ' ';//匹配时，输出 模式串首元素在主串中的下标
j = ne[j];//j后滑，准备继续寻找下一个匹配处
}
}
return 0;
}
字符串从数组下标为开始存
const int N = 1000010;
char s[N], p[N];
int ne[N];
int main()
{
int n, m;
cin >> m >> p >> n >> s;
ne[0] = -1;//ne[0]初始化为-1
for (int i = 1, j = -1; i < m; i ++ )//从模式串的第2位2开始求next值
{
while (j != -1 && p[j + 1] != p[i]) j = ne[j];
if (p[j + 1] == p[i]) j ++ ;
ne[i] = j;
}
for (int i = 0, j = -1; i < n; i ++ )//遍历一遍主串
{
while (j != -1 && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m - 1)//扫描到模式串结尾，说明匹配完成
{
cout << i - j << ' ';
j = ne[j];
}
}
return 0;
}
总结
本篇文章就到这里了，希望能够给你带来帮助，也希望您能够多多关注html5模板网的更多内容！
VS2019中在源文件中如何使用自己写的头文件通过头文件的形式直接调用自定义的函数，从而免去对函数的原型进行声明，本文就详细的介绍一下VS2019中在源文件中如何使